日常教学中发现，很多同学平面向量学得不好的原因主要是没掌握、没理解平面向量基本定理、向量共线定理和平行向量（共线向量）。

平行向量和共线向量是平面向量的一个重难点，也是一个疑难点。掌握平面向量是掌握后续重点——向量共线定理的一个重要前提。掌握向量共线定理是理解后面另一个重难点——平面向量基本定理的前提。

学不好平行向量和共线向量是学不好平面向量的一个重要原因。所以毫不夸张地说，是否掌握了平行向量和共线向量，决定了能否掌握平面向量这个高考的高频考点。

一、平行向量与共线向量的关系

平行向量又叫共线向量，二者是一回事。

二、本文从两个角度来帮大家彻底理清平行向量的概念

角度一、图形角度

从图形角度来分类，两向量平行（共线）有且只有两种情况：

1. 两向量所在直线平行。换句话说就是，只要是两条平行直线上的两个向量，都可互称为平行向量（共线向量），与二者的位置、方向相同还是相反无关。
2. 两向量所在直线重合。换句话说就是，只要两个向量所在直线重合（或是同一条直线上的两个向量），则这两个向量互称为平行向量（共线向量）。与二者的位置、方向相同还是相反无关。

例：已知下图中的两条直线（虚线）平行，则下图中出现的三个向量，任何两个向量间都可以互称为平行向量。

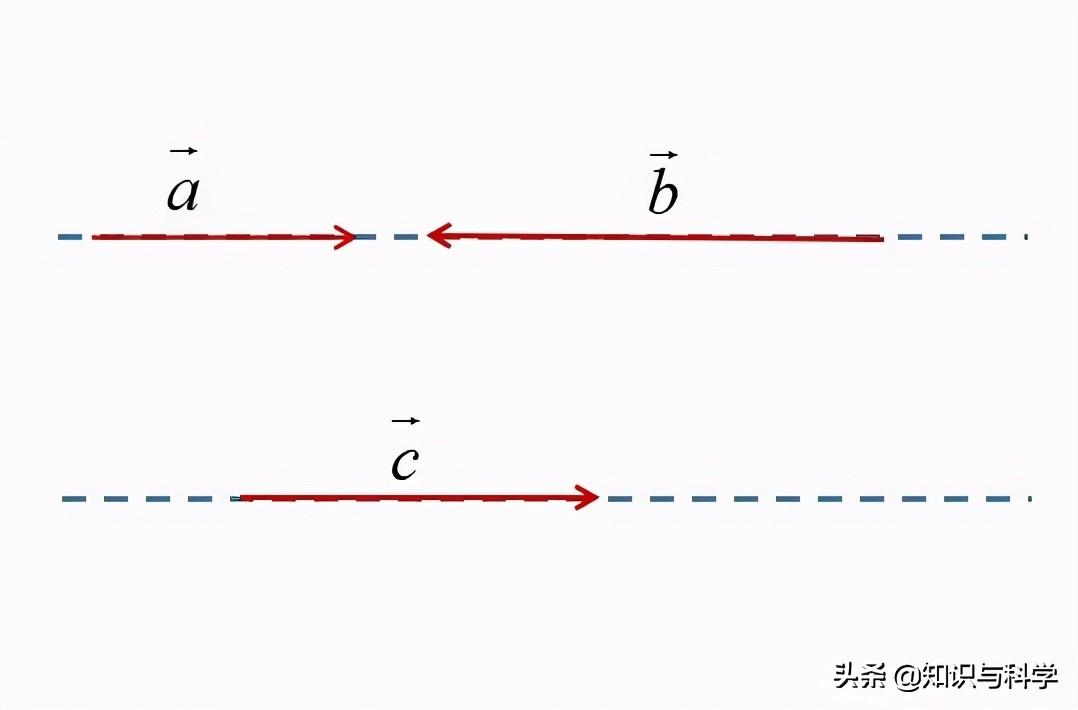
平行向量（共线向量）的图示

【注】1.向量间的平行不同于直线间的平行。位于同一条直线上的两个向量也可互称为平行向量（共线向量）。2.向量的“共线”，不同于直线的“共线”。不在同一直线上的两个平行向量也可互称为共线向量（平行向量）。

角度二、方向角度

从方向的角度来分类，两向量平行（共线）也是有且只有两种情况：

1. 两向量的方向相同（同向）。换句话说就是，只要方向相同的两个向量都可互称为平行向量（共线向量），与它们的位置和模长无关。
2. 两向量的方向相反（反向）。换句话说就是，只要方向相反的两个向量都可互称为平行向量（共线向量），与它们的位置和模长无关。

最后有一种特殊情况，就是零向量。

零向量的方向是任意的。规定：零向量与任意向量平行。

【注】只有非零向量间的平行（共线）才一定具有传递性。如下面两个例题所示：

只有非零向量间的共线才具有传递性

平行向量=共线向量，在判断两向量是否平行（共线）时，有图形角度和方向角度。这两个角度在本质上是内在统一的。同学们做题时可以根据不同的题型和自己的需要来灵活地选择不同的判断方法。