
三角形是初中几何部分非常重要的一个板块。其基础性较强,是学习多边形,四边形,甚至其他几何图形的桥梁。之所以这样说,其他图形的学习过程中都是以三角形作为研究对象,甚至与三角形有密切的联系。作为基础性较强的三角形部分,其涉及到的概念知识比较多,只有将这些基础的概念理解到位,那么在掌握基础方面才能抓住先机,同时也能为学习其他的内容打下坚实的基础。
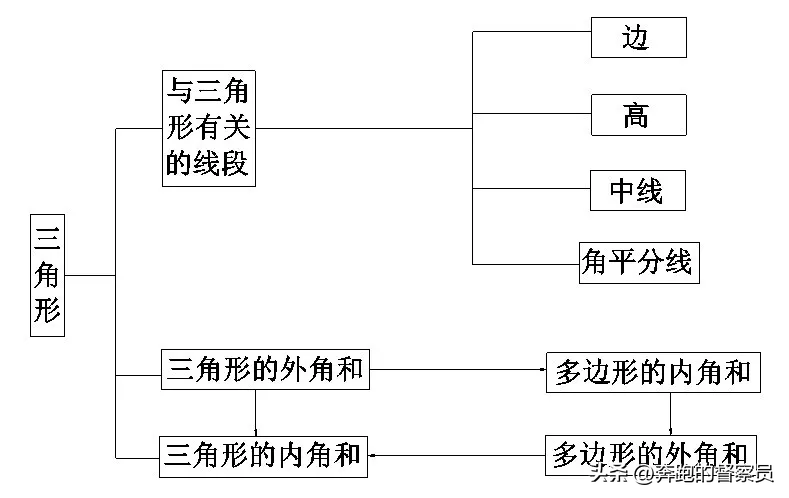
在学习三角形部分是大家先以这些基础的概念进行理解,然后再以这些基础的概念进行相对应性质的拓展,而且往往很多题型都是靠其性质而打开突破口的。比如三角形的高,既可以推断出线段的垂直,也可以得到两个直角三角形。这样初步的推理,对下一步解题当中可能用到的性质也是一目了然。

1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.
3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫作三角形的高.
4.中线:在三角形中,连接一个顶点和它对边中点的线段叫作三角形的中线.
5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫作三角形的角平分线.

其次,在学完有关三角形的高,角平分线和中线等线段后,可以集中将这几类线段进行初步的归纳,处理其涉及到的知识点以及角度的计算都是这部分内容经常考察的内容,然后再配合相对应的题型进行集中的训练,相信三角形的这几类线段的性质就能达到熟练使用的地步。当然同学们也可以通过画一个三角形,将三角形内的这些线统一地划在一个三角形内,这样能够清楚地分辨出各线段之间的区别。

6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.
7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫作多边形.
8.多边形的内角:多边形相邻两边组成的角叫作它的内角.
9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫作多边形的外角.
10.多边形的对角线:连接多边形相邻的两个顶点的线段,叫作多边形的对角线.
11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.
12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫作用多边形覆盖平面。

第三,在三角形学习的基础之上进行拓展学习多边形都是以三角形的内容为基础而展开的,所以美学一种多边形的性质和特点都要和三角形的性质和特点挂钩,所以三角形性质和概念的理解对于学习多边形也起到了积极的促进作用。
13.公式与性质:
⑴三角形的内角和:三角形的内角和为180°
⑵三角形外角的性质:
性质1:三角形的一个外角等于和它不相邻的两个内角的和.
性质2:三角形的一个外角大于任何一个和它不相邻的内角.
⑶多边形内角和公式:边形的内角和等于·180°
⑷多边形的外角和:多边形的外角和为360°.
⑸多边形对角线的条数:
①从边形的一个顶点出发可以引条对角线,把多边形分成两个三角形.
②边形共有条对角线.

最后,对于三角形这一章节中涉及到的公式和运算的方法是对于三角形基础上而展开的角的计算,在实际的考察题型当中也是最为普遍和考察频率较高的内容,同学们需要以三角形内角和和外角和的特点出发来探究多边形的特点,从而发现其中的规律,那么这些公式也就完全能够融合到一起。
写在最后,三角形有关概念的集合对于学习三角形或多边形的内容都是具有基础意义的,将为后续多边形甚至几何的其他部分学习打下坚实基础,理解透彻的情况下,其学习的效率也会更高,这其中所运用到的方法以及各线段,各图形与三角形的关系,都是我们建立几何框架的基础,内容及意义也是不容小觑。