

第一单元 《观察物体三》
1、根据一个方向观察到的形状摆小正方体,有多种摆法,无法确定立体图形的形状。
2、根据三个方向观察到的形状摆小正方体,只有1 种摆法。
3、从正面、左面、上面3个不同的方向观察同一组物体而画出的图形就是三视图。
5、由三视图拼摆正方体的方法:俯视图打地基,主视图疯狂盖,左视图拆违章。
6、先摆出符合正面的立体图形,再摆出符合上面的立体图形,最后确定立体图形。根据从正面、左面、上面观察到的平面图形还原立体图形只有唯一的一种情况。
7、不同角度观察一个物体 , 看到的面都是两个或三个相邻的面。
8、至少用8个正方体可拼成较大的正方体,27个64个125个……都可拼成较大正方体。
第二单元 因数和倍数
一、因数和倍数。
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数的倍数,除数是被除数的因数.
如整数a能被b整除(a÷b=c),那么a就是b和c的倍数,b和c就是a的因数。因数和倍数是相互依存的,不能单独存在。
因数:一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身。
如:9的最小的因数是1,最大的因数是9。
又如:A的最小的因数是1,最大的因数是A。
一个数的因数的求法:成对地按顺序找,或用除法找。
如:15的因数:1、3、5、15
方法:15÷1=15,15÷3=5 (除法)
或 15=1×15 15=3×5 (乘法)
完全数:除了它本身以外所有的因数的和等于它本身的数叫做完全数。如:6的因数有:1、2、3(6除外),刚好1+2+3=6,所以6是完全数,小的完全数有6、28等
倍数:一个数的倍数的个数是无限的,最小的倍数是它本身。
一个数的倍数的求法:依次乘自然数。
例如:6的倍数:6,12,18,24,30……
方法:6×1=6,6×2=12,6×3=18,
6×4=24,6×5=30,6×6=36……
二、自然数按能不能被2整除分为:奇数 偶数
奇数:不是2的倍数的数叫做奇数。
如1、3、5、7、9、11……
偶数:是2的倍数的数叫做偶数。
如:2、4、6、8、10、12……
最小的奇数是1,最小的偶数是0。
2、3、5倍数的特征:
个位上是0,2,4,6,8的数都是2的倍数。
个位上是0或5的数,是5的倍数。
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
如果一个数同时是2和5的倍数,那它的个位上的数字一定是0。
同时是2、3、5的倍数,个位上是0并且各位上的数的和是3的倍数,这个数就同时是2、3、5的倍数。最大的两位数是90,最小的两位数是30,最小的三位数是120。
同时满足2、3、5的倍数,实际是求2×3×5=30的倍数。
6的倍数既是2 的倍数,又是3的倍数。
(个位上是0,2,4,6,8且各位上的数的和是3的倍数)
同时是3、5的倍数的特征:个位上是0或5,且各位上的数的和是3的倍数。
三、自然数按因数的个数来分:质数、合数、1、0.
质数:一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
如2,3,5,7,11,13,17,19……都是质数。
合数:一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,8,9,10,12,14,15,16,18,20,22,26,49……都是合数。合数至少有三个因数,1、它本身、别的因数
1: 只有1个因数。“1”既不是质数,也不是合数。
最小的质数是2,最小的合数是4。
20以内的质数:有8个(2、3、5、7、11、13、17、19)
(1)所有的奇数都是质数。不对,因为9是奇数,但不是质数,而是合数。
(2)所有的偶数都是合数。不对,因为2是偶数,但不是合数,是质数。
(3)在1,2,3,4,5,…中,除了质数以外都是合数。不对,因为1既不是质数也不是合数。(4)两个质数的和是偶数。不对,因为2是质数也是偶数,而其他的质数都是奇数,偶数+奇数=奇数。
四、100以内的质数(共 25 个):2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97
五,奇数+奇数=偶数(如:5+7=12 3+5=8)
奇数+偶数=奇数(如:1+4=5 7+2=9)
偶数+偶数=偶数(如:2+4=6 8+6=14)
奇数×奇数=奇数(如:5×7=35 7×9=63)
奇数×偶数=偶数(如:5×8=40 7×8=56)
偶数×偶数=偶数(如:8×12=96 14×24=336)
质数×质数=合数
分解质因数:把一个合数分解成多个质数相乘的形式。
用短除法分解质因数 (一个合数写成几个质数相乘的形式)。
比如:30分解质因数是:(30=2×3×5)
六、公因数、最大公因数
几个数公有的因数叫这些数的公因数。其中最大的那个因数就叫它们的最大公因数。用短除法分解质因数 (一个合数写成几个质数相乘的形式)例:12=2×2×3
用短除法求两个数或三个数的最大公因数 (除到互质为止,把所有的除数连乘起来).

几个数的公因数只有1,就说这几个数互质。两数互质的特殊情况:
⑴1和任何自然数互质;
⑵相邻两个自然数互质;
⑶两个质数一定互质;
⑷2和所有奇数互质;
⑸质数与比它小的合数互质;
如果两数是倍数关系时,那么较小的数就是它们的最大公因数。
如果两数互质时,那么1就是它们的最大公因数。
两个数的公因数是它们最大公因数的因数。
七、公倍数、最小公倍数:几个数公有的倍数叫这些数的公倍数。其中最小的那个就叫它们的最小公倍数。
用短除法求两个数的最小公倍数(除到互质为止,把所有的除数和商连乘起来)
用短除法求三个数的最小公倍数(除到两两互质为止,把所有的除数和商连乘起来)

如果两数是倍数关系时,那么较大的数就是它们的最小公倍数。
如果两数互质时,那么它们的积就是它们的最小公倍数。
两个数的公倍数是它们最小公因倍数的倍数。
互质数:公因数只有1的两个数,叫做互质数。
两个质数的互质数:5和7
两个合数的互质数:8和9
一质一合的互质数:7和8
求最大公因数和最小公倍数方法
用12和16来举例
1、 求法一:(列举求同法)
最大公因数的求法:
12的因数有:1、12、2、6、3、4
16的因数有:1、16、2、8、4
最大公因数是4
最小公倍数的求法:
12的倍数有:12、24、36、48、…
16的倍数有:16、32、48、…
最小公倍数是48
2、求法二:(分解质因数法)
12=2×2×3
16=2×2×2×2
最大公因数是:2×2=4 (相同乘)
最小公倍数是:2×2×3×2×2= 48 (相同乘× 不同乘)
3、求法三:短除法
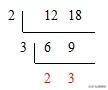
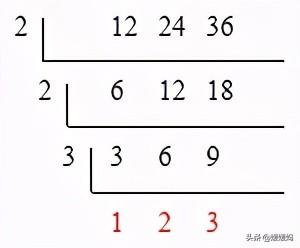
用短除法求下列各组数的最大公因数。①12和18 ②34和102 ③ 12、24和36
想:用短除法求两个数的最大公因数,一般用这两个数除以它们的公因数,一直除到所得的两个商只有公因数1为止,再把所有的除数连乘起来,所得积就是这两个数的最大公因数。最小公倍数就是所有公因数连乘再乘最后的商。

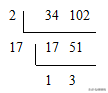
34和102的最大公因数是 2×17=34,
最小公倍数是 2×17×1×3=102

最大公因数和最小公倍数的知识应用:
1:一张长方形纸长24厘米,宽16厘米,如果要剪成若干同样大小的正方形而没有剩余,剪出的正方形的边长最大是多少厘米?可以剪几个正方形?
解题思路:正方形的边长一定是长和宽的公因数,且是最大公因数。
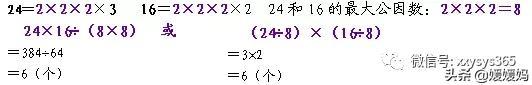
答:剪出的正方形的边长最大是8厘米。可以剪6个正方。
最大公因数的应用的关键词:“最大”、“最长”、“最多”等。
知识应用2:甲、乙两人去图书馆看书,甲每6天去一次,乙每8天去一次。如果4月1日他们两个在图书馆相遇,那么下一次在图书馆相遇是几月几日?
解题思路:他们两个下次在图书馆相遇所经过的天数一定是6和8的公倍数,且是最小公倍数。
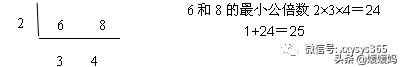
答:他们下一次在图书馆相遇是4月25日。
知识应用3:一群学生去春游,去时12个人坐一辆车刚好,回来时8个人坐一辆车刚好。这群学生最少有多少人?
解题思路:12刚好8也刚好,那么总人数一定是8和12的公倍数,最少多少人就是求最小公倍数。
12=2×2×3 8=2×2×2 最小公倍数 2×2×3×2=24
答:这群学生最少有24人。
最小公倍数的应用的关键词:“最少”、“最小”、“至少”等。

第三单元 长方体和正方体
1、由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。长方体和正方体都是立体图形。正方体也叫立方体。
2、相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。(长、宽、高都各有4条,分别平行并且相等)
3、长方体的特征:
① 面:有6个面,都是长方形(特殊情况下最多有两个相对的面是正方形)。相对的面完全相同。
② 棱:有12条棱。相对的棱长度相等。
③ 顶点:有8个顶点。
4、正方体的特征:
① 面:有6个面都是正方形,6个面完全相同。
② 棱:有12条棱。12条棱的长度相等。
③ 顶点:有8个顶点。
相同点 | 不同点 | ||
面 | 棱 | ||
长方体 | 6个面, 12条棱, 8个顶点。 | 6个面都是长方形。(有可能有两个相对的面是正方形)。 | 相对的棱的长度都相等 |
正方体 | 6个面都是正方形。 | 12条棱都相等。 | |
5、正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
至少要8个小正方体才能拼成一个稍大的正方体。
经过折叠可以组合成长方体:

长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4
L=(a+b+h)×4 (长+宽+高)=棱长总和÷4
长=棱长总和÷4-宽 -高 a=L÷4-b-h
宽=棱长总和÷4-长 -高 b=L÷4-a-h
高=棱长总和÷4-长 -宽 h=L÷4-a-b
经过折叠可以组合成正方体:
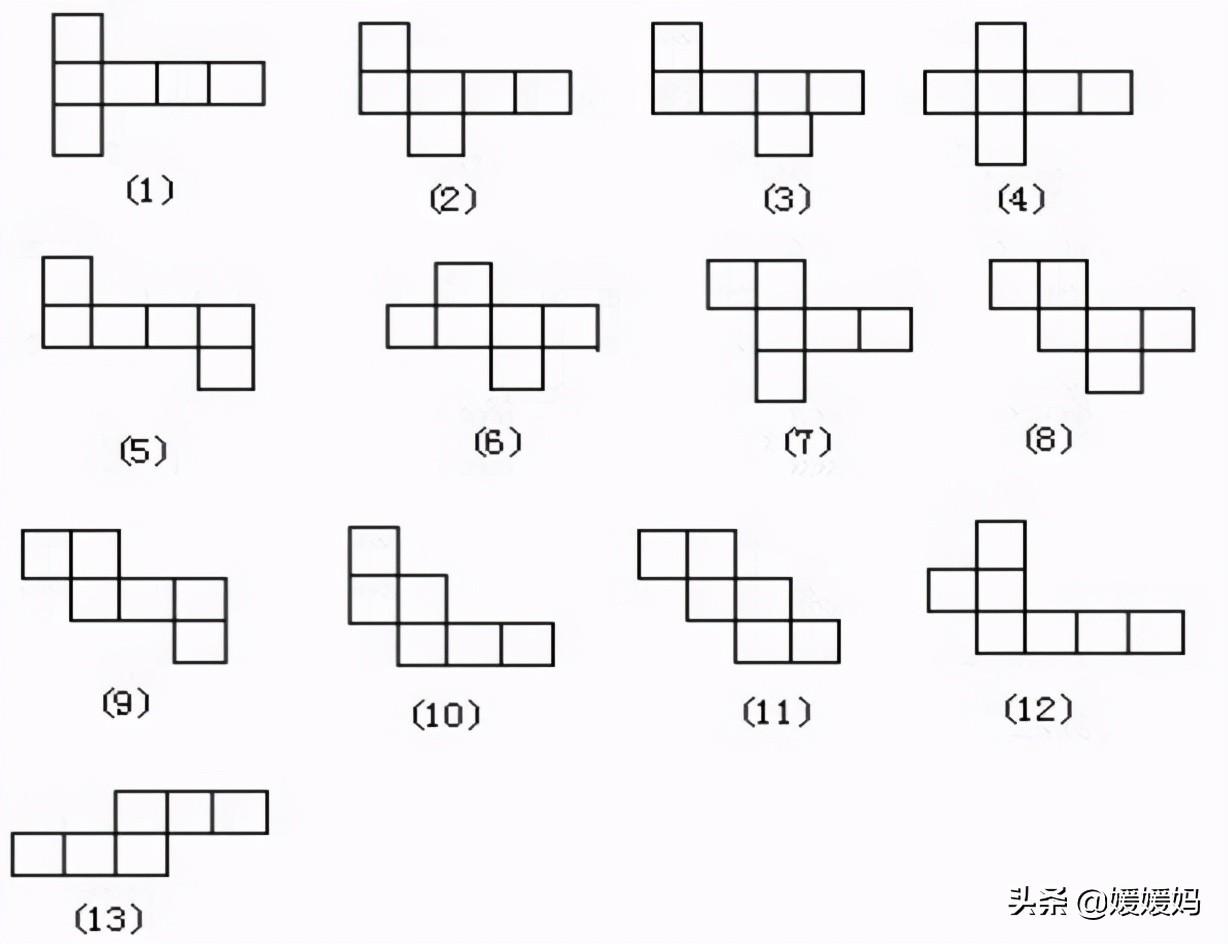
正方体的棱长总和=棱长×12 L=a×12
正方体的棱长=棱长总和÷12 a=L÷12
6、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
无底(或无盖)长方体表面积= 长×宽+(长×高+宽×高)×2
S=2(ab+ah+bh)-ab 或 S=ab+2ah+2bh
S=2(ah+bh)+ab
无底又无盖长方体表面积=(长×高+宽×高)×2 S=2(ah+bh)
正方体的表面积=棱长×棱长×6
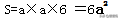
生活实际:占地面积是指底面积 S=a×b
油箱、罐头盒等都是6个面 S=2(ab+ah+bh)
游泳池、鱼缸、教室涂刷等都只有5个面。(S=ab+2ah+2bh)
水管、烟囱等都只有4个面。S=a×a×4 =4a²
注意1:用刀分开物体时,每分一次增加两个面。(表面积相应增加)
注意2:长方体或正方体的长、宽、高同时扩大几倍,表面积会扩大倍数的平方倍。(如长、宽、高各扩大2倍,表面积就会扩大到原来的4倍)
7、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V÷b÷h
宽=体积÷长÷高 b=V÷a÷h
高=体积÷长÷宽 h= V÷a÷b 或 h= V÷S
正方体的体积=棱长×棱长×棱长
V=a×a×a = a³ 读作“a的立方”表示3个a相乘,(即a·a·a)
长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高 用字母表示:V=S h
(横截面积相当于底面积,长相当于高)。
注意:一个长方体和一个正方体的棱长总和相等,但体积不一定相等。
长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高 用字母表示:V=S h
(横截面积相当于底面积,长相当于高)。
注意:一个长方体和一个正方体的棱长总和相等,但体积不一定相等。
8、箱子、油桶、仓库等容器所能容纳物体的体积,通常叫做他们的容积。
长方体和正方体容器容积的计算方法,跟体积的计算方法相同,但要从里面量长、宽、高。(所以物体的体积大于它的容积)。
常用的容积单位有升和毫升也可以写成L和ml。
1升=1立方分米 1毫升=1立方厘米
1升=1000毫升
(1 L = 1 dm³ 1 ml = 1 cm³)
9、注意:长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
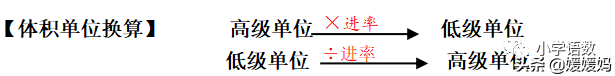


注意:长方体与正方体关系
把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。

10、长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
11、排水法:(计算不规则物体的体积)

形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:V物体 =V现在-V原来
也可以 V物体 =S×(h现在- h原来)
V物体= S×h升高
例1:把一石块放入一个长10dm宽6dm高5dm的长方体玻璃缸中,水面升高1.5dm,求石块的体积是多少?
V物体= S×h升高=10×6×1.5
例2:把6L水放入一个长3dm宽2dm高3dm的长方体玻璃缸中,再沉入一块石头,量得水面高1.5dm,求石头的体积是多少?
6L=6dm³
V物体 =V水和物的总体积-V水=3×2×1.5-6
例3:在一个长3dm宽2dm高3dm的长方体玻璃缸中,量得水面高1.5dm,沉入一块石头后,量得水面高2dm,求石头的体积是多少?
V物体=V现在-V原来
=3×2×2-3×2×1.5
12、把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
第四单元 分数的意义和性质
1、单位“1”表示:一个物体、一个计量单位或是一些物体都可以看成一个整体。这个整体可以用自然数1来表示,我们通常把它叫做单位“1” (也就是把什么平均分什么就是单位“1”。)
2、把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。


5、分数大小的比较:
分母相同的两个分数,分子大的分数较大。
分子相同的两个分数,分母小的分数较大。
异分母分数,先化成同分母分数(分数单位相同),再进行比较。
6、真分数和假分数:真分数分子比分母小的分数叫做真分数。真分数比1小。
假分数分子比分母大或分子和分母相等的分数叫做假分数。假分数≧1
假分数大于1或等于1。(真分数<1≤假分数 真分数<1<带分数)
带分数:带分数由整数和真分数组成的分数。带分数>1.
把假分数化成整数或带分数:用分子÷分母。
能整除的,所得的商就是整数;不能整除的,所得的商就是带分数的整数部分,余数是就是分数部分的分子,分母不变。
假分数化为整数或带分数,用分子÷分母,商作为整数,余数作为分子, 如:
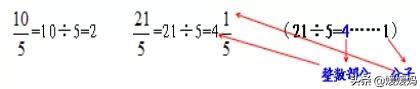
整数化为假分数,用整数乘以分母得分子. 如:
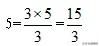
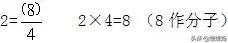
带分数化为假分数,用整数乘以分母加分子,得数就是假分数的分子,分母不变.
如:
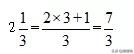
1等于任何分子和分母相同的分数。如:
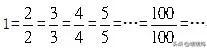
7、分数的基本性质——分数的分子和分母同时乘上或除以相同的数(0除外),分数的大不变。
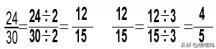
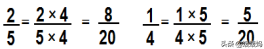
8、约分——把一个分数化成同它相等,但分子、分母都比较小的分数,叫做约分。(方法就是分子和分母同时除以它们的公因数。)如:
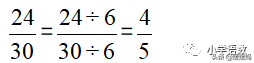
分子、分母是互质数的分数,叫做最简分数。
应用:填最简分数:

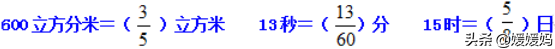
9、通分——把异分母分数化成和原来分数相等的同分母的分数,叫做通分。方法:先求出原来几个分母的最小公倍数,再根据分数的基本性质把各个分数化成用这个最小公倍数作公分母的分数。如:
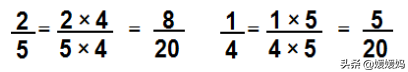
10、分数和小数的互化。
小数化成分数:原来有几位小数,就在1后面写几个0作分母,把原来的小数去掉小数点作分子;化成分数后,能约分的要约分。
小数化为分数:数小数位数。一位小数,分母是10;两位小数,分母是100……
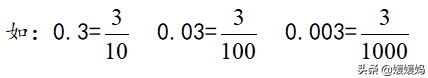
分数化小数:用分子除以分母,除不尽的按要求保留几位小数。(一般保留两位小数。)
分数化为小数:
方法一:把分数化为分母是10、100、1000……
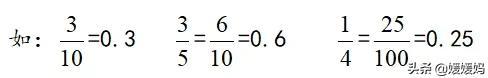
方法二:用分子÷分母
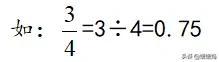

带分数化为小数:
先把整数后的分数化为小数,再加上整数
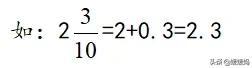
或把带分数化成假分数后,用分子除以分母,如:
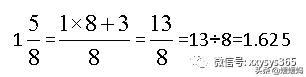
判断分数是否能化成有限小数的方法:
① 判断分数是否是最简分数;如果不是最简分数,先把它化成最简分数;
② 把分数的分母分解质因数:
如果分母中除了2和5以外,不含有其他质因数,这个分数就能化成有限小数;
如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数。
11、分数化简包括两步:一是约分;二是把假分数化成整数或带分数。

两个数互质的特殊判断方法:
① 1和任何大于1的自然数互质。
② 2和任何奇数都是互质数。
③ 相邻的两个自然数是互质数。
④ 相邻的两个奇数互质。
⑤ 不相同的两个质数互质。
⑥当一个数是合数,另一个数是质数时(除了合数是质数的倍数情况下),一般情况下这两个数也都是互质数。
12、比分数的大小:
分母相同,分子大,分数就大;

分子相同,分母小,分数才大。

分数比较大小的一般方法:同分子比较;通分后比较;化成小数比较。
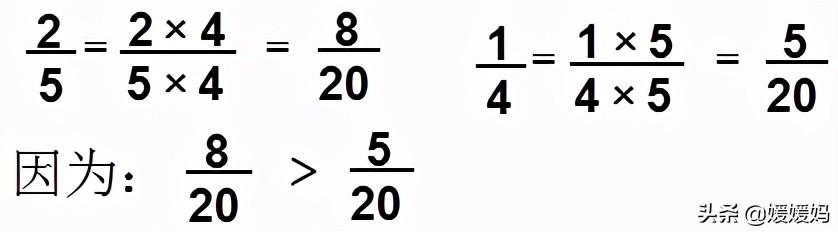
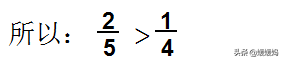
第五单元 图形的运动(三)
图形变换的基本方式是对称、平移和旋转。
对称点是关于一条直线对称的点 (对称点一般用于轴对称), 对应点是一个图形经变换后的图形与变换前的图形位置相同的点(对应点一般用于平移和旋转)
(一)图形的平移
1、平移不改变图形的大小和形状。
2、平移的三要素:原图形的位置、平移的方向、平移的距离。
平移的方向一般为:水平方向、垂直方向两种。
平移的距离:一般为几个单位长度(也即几个方格)
3、平移是整个图形的移动,图形的每个关键点都需要按要求移动。
4、把图形平移的步骤:
(1)确定原图形位置、平移的方向、平移的距离。
(2)找出原图形的各关键点。
(3)根据题目要求将各个点依次平移。
(4)顺次连接平移后的各点,标明各点名称。
(二)轴对称: 如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
(1)学过的轴对称平面图形有:圆形、长方形、正方形、圆形、等腰三角形、等边三角形、等腰梯形……
等腰三角形有1条对称轴,等边三角形有3条对称轴,长方形有2条对称轴,正方形有4条对称轴,等腰梯形有1条对称轴,圆有无数条对称轴。任意梯形和平行四边形不是轴对称图形。
(2)对称点到对称轴的距离相等。
(3)轴对称图形的特征和性质:
①对称点到对称轴的距离相等;
②对称点的连线与对称轴垂直;
③对称轴两边的图形大小、形状完全相同,方向相反。
(4)对称图形包括轴对称图形和中心对称图形。平行四边形(除棱形)属于中心对称图形。
2、旋转:物体或图形围绕一个定点沿着一个方向转动一定的角度的现象叫做旋转。如风扇的叶片旋转。定点O叫做旋转中心,旋转的角度叫做旋转角,原图形上的一点旋转后成为的另一点成为对应点。
(1)生活中的旋转:电风扇、车轮、纸风车
(2)旋转三要素:
①旋转中心,固定不变;
②旋转方向有顺时针、逆时针;
③旋转角度有:常见的有30°、45°、60°、90°、180°、270°。
(3)长方形绕中心点旋转180度与原来重合,
正方形绕中心点旋转90度与原来重合。
等边三角形绕中点旋转120度与原来重合。
(4)旋转的性质:
①图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;
②其中对应点到旋转中心的距离相等;旋转前后图形的大小和形状没有改变,位置和方向发生改变,旋转中心是唯一不动的点;
③两组对应点分别与旋转中心的连线所成的角度相等,都等于旋转角;
(5)怎样画图形旋转的形状:
①先观察原图形的形状特征找准关键点;
②找准旋转中心、旋转方向、旋转角度 ;
③使用直角三角板的顶点与旋转中心重合,则该图形旋转后的形状就在三角板另一条边上;
④确定各对应点的长度,用虚线标出来;
⑤将每个对应点连接并标出名称。
3、对称和旋转的画法:旋转要注意:顺时针、逆时针、度数。
第六单元 分数的加法和减法
具体解释
(一)同分母分数加、减法
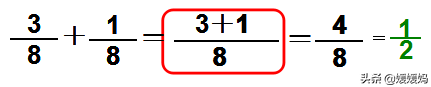
1、同分母分数加、减法:
同分母分数相加、减,分母不变,只把分子相加减。
2、计算的结果,能约分的要约成最简分数。是假分数的一般要化成带分数或整数。

3、带分数加减法: 带分数相加减,整数部分和分数部分分别相加减,再把所得的结果合并起来。
(二)异分母分数加、减法
1、分母不同,也就是分数单位不同,不能直接相加、减。
2、异分母分数的加减法:
异分母分数相加、减,要先通分,再按照同分母分数加减法的方法进行计算。
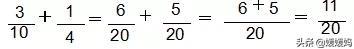
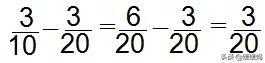
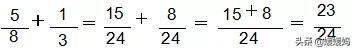
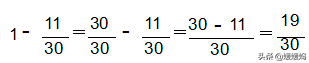
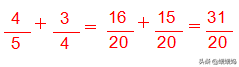
(三)分数加减混合运算
1、分数加减混合运算的运算顺序与整数加减混合运算的顺序相同。
在一个算式中,如果有括号,应先算括号里面的,再算括号外面的;如果只含有同一级运算,应从左到右依次计算。

2、整数加法的交换律、结合律对分数加法同样适用 a+b=b+a a+b+c=a+(b+c)
3、
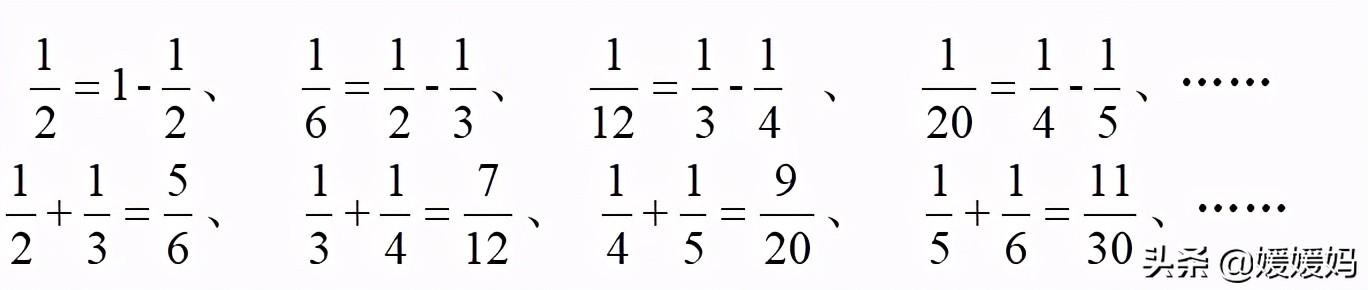
4、减法的性质:a-b-c=a-(b+c) a-(b-c)=a-b+c= a+c –b(等式左右可以交换的)
5、常见乘法计算(敏感数字) :
25×4=100 125×8=1000


去括号或添括号:
加减混合时, 括号前是加号的,去掉括号后,括号内的符号不变号;
括号前是减号的,去掉括号后,括号内的符号要变号。
如:
30+85—65=30+(85—65)
85—60+30=85—(60—30)
6、解方程
解方程方法一:运用四则运算各部分之间的关系来解方程
加数+加数=和、和— 一个加数=另一个加数 、
被减数—减数=差、被减数=差+减数 、减数=被减数—差
因数×因数=积、一个因数=积÷另一个因数
被除数÷除数=商、除数=被除数÷商、被除数=商×除数
解方程方法二:消项(如果消+3,方程两边就同时-3 ;如果消×3,方程两边就同时÷3)
解方程方法三:移项(+3移到另一边就变成-3,×3移到另一边就变成÷3)

7、打电话
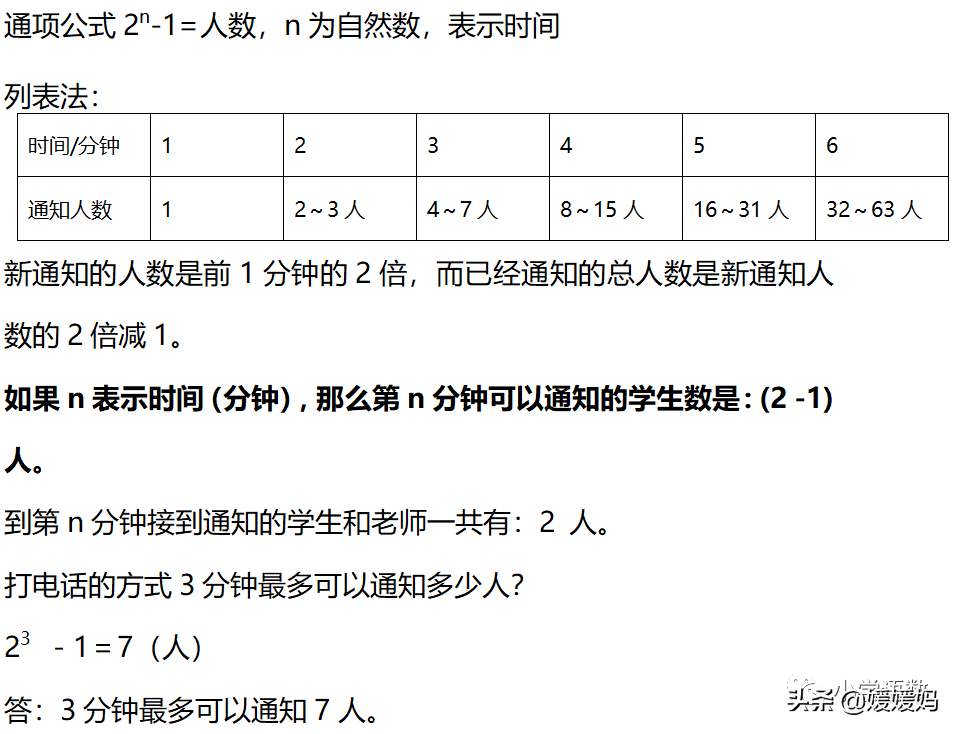

第七单元 折线统计图
折线统计图
1、 画图时注意:一“点”(描点)、 二“连”(连线) 三“标”(标数据)
2、 复式折线统计图:要用不同的线段分别连接两组数据中的数。
统计图:我们学过条形统计图、复式折线统计图。
条形统计图优点:条形统计图能形象地反映出数量的多少。
折线统计图优点:折线统计图不仅能表示出数量的多少,还能反映出数量增减的变化情况以及发展趋势(呈上升或下降的趋势)。

3、单式折线统计图通过将一组数据的水平表示出来,可以很容易地看出数量增减变化的情况。
复式折线统计图通过两组以上数据的水平进行比较,可以容易地比较出两组以上数据的变化趋势,更清楚看出各类之间的比较。
知识应用:
1、选择题。

2、统计图分析。
A、根据下面的统计图,回答问题
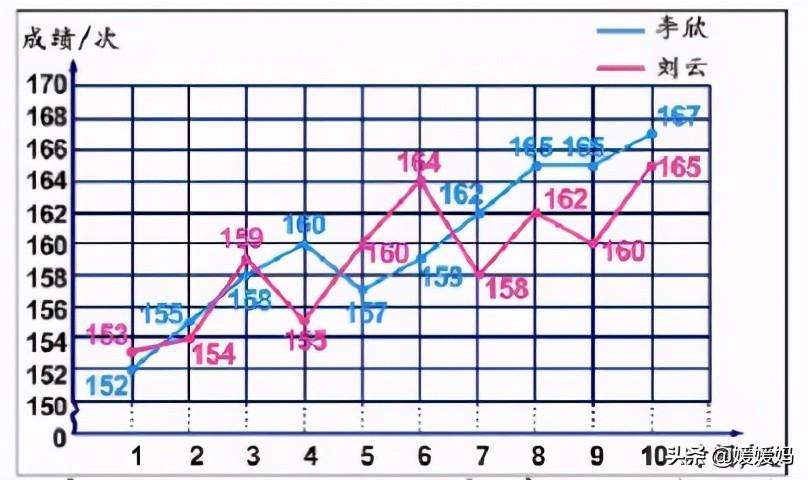


B、下面是某地区7—15岁男生、女生平均身高的统计图。
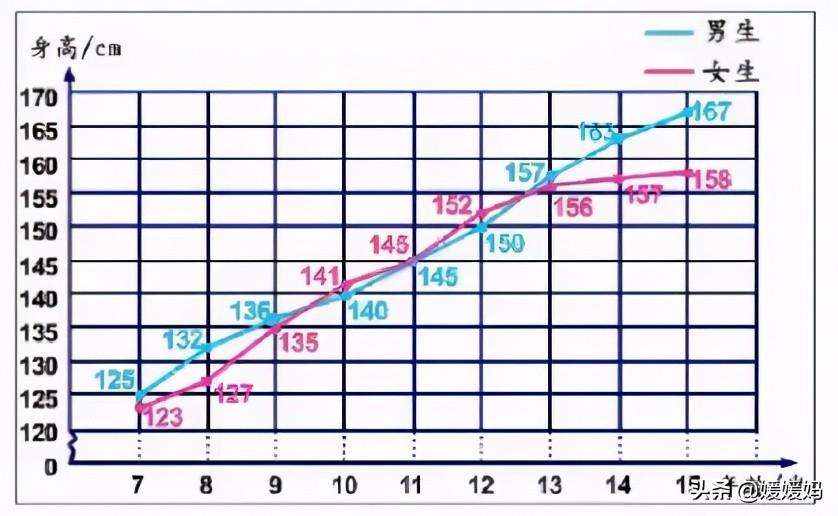

答:男、女生的平均身高都随着年龄增加面增高,但是女生13岁后的增长趋于平缓,增长速度要比男生的速度慢。
C、根据下面的统计图,回答问题
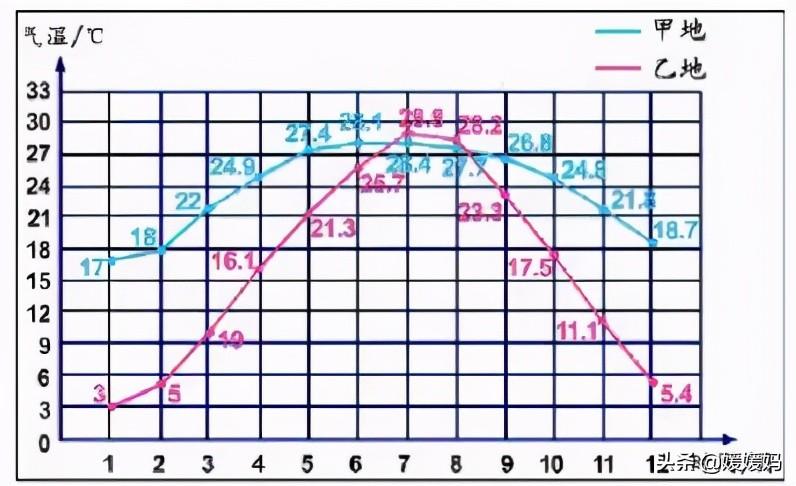
1、根据统计图,你能判断一年气温变化的趋势吗?
答:甲、乙两地的气温都是先上升后下降。
甲地一年气温变化趋势较大,7月份温度最高。
乙地一年气温变化趋势较平稳,7月份温度最高。
2、有一种树莓的生长期为5个月,最适宜的生长温月为7~10摄氏度之间,这种植物适合在哪个地方种植?
答:这种植物适合在乙地种植。
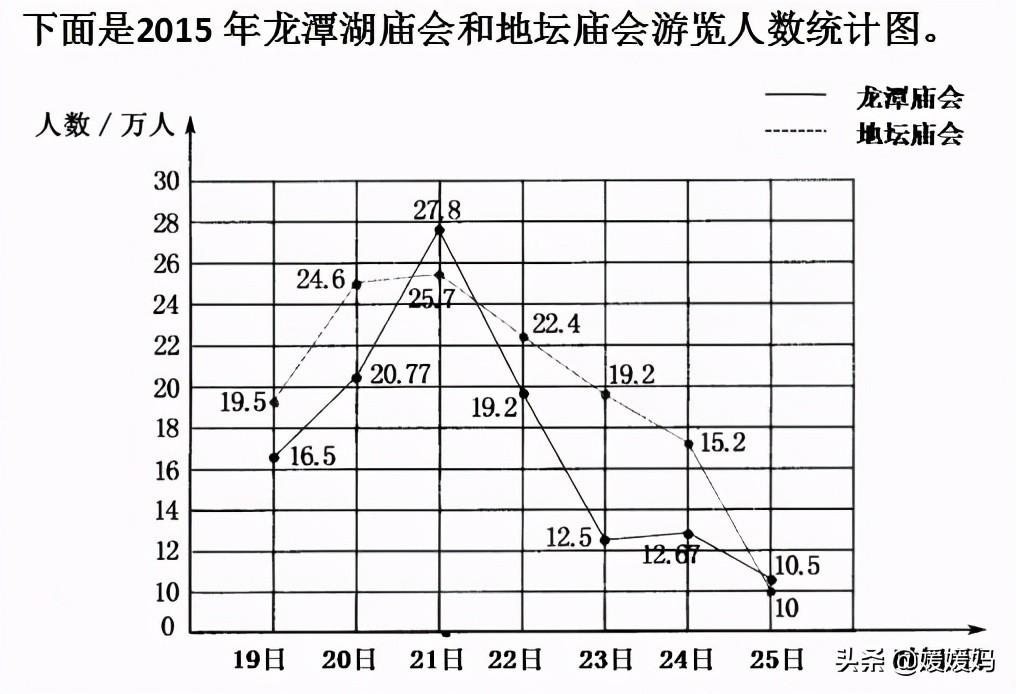
D、根据下面的统计图,回答问题

第八单元 数学广角
用天平找次品规律:
1、把所有物品尽可能平均地分成3份,(如余1则放入到最后一份中;如余2则分别放入到前两份中),保证找出次品而且称的次数一定最少。
2、数目与测试的次数的关系:
2~3个物体,保证能找出次品需要测的次数是1次
4~9个物体,保证能找出次品需要测的次数是2次
10~27个物体,保证能找出次品需要测的次数是3次
28~81个物体,保证能找出次品需要测的次数是4次
82~243个物体,保证能找出次品需要测的次数是5次
244~729个物体,保证能找出次品需要测的次数是6次
3、找次品规律

小学数学平面图形周长、面积计算公式
一、正方形(a表示边长,C表示周长,S表示面积)
正方形的周长=边长×4 C=4a
正方形的面积=边长×边长 S=a×a
二、长方形(a表示长,b表示宽,C表示周长,S表示面积)
长方形的周长=(长+宽)×2
字母表示为:C=(a+b)×2
长方形的面积=长×宽
字母表示为:S=a×b
三、三角形(s表示面积a表示底h表示高)
三角形的面积=底×高÷2
字母表示为:s=a×h÷2
三角形的高=面积×2÷底
字母表示为:h = s×2÷a
三角形的底=面积×2÷高
字母表示为:a = s×2÷h
四、平行四边形(a表示底,h表示高,S表示面积)
平行四边形的面积=底×高
字母表示为:S= a×h
平行四边形的高=面积÷底
字母表示为:h= s÷a
平行四边形的底=面积÷高
字母表示为:a= s÷h
五、梯形(s表示面积,a表示上底,b表示下底,h表示高。)
梯形的面积=(上底+下底)×高÷2
字母表示为:s=(a+b)×h÷2
梯形的(上底+下底) =面积×2÷高
字母表示为:a+b = s×2÷h
梯形的高=面积×2÷(上底+下底)
字母表示为:h = s×2÷a+b