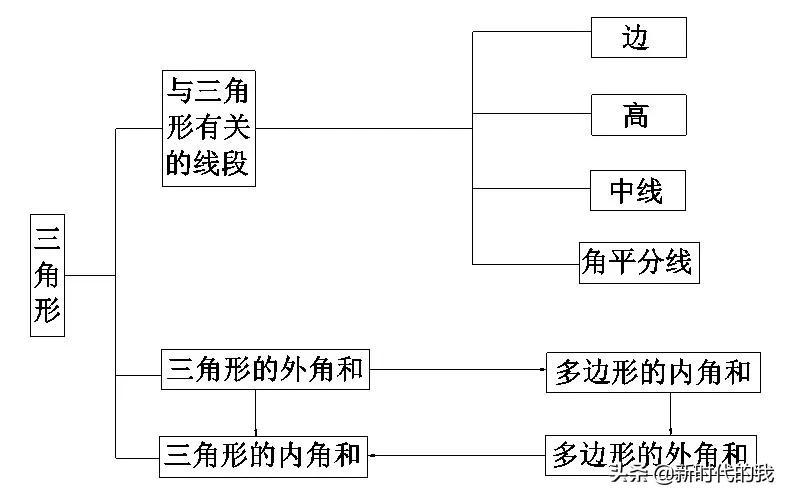
与三角形有关的线段知识点
一、三角形的有关概念
1、三角形的边
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
相邻两边组成的角,叫做三角形的内角,简称三角形的角。
顶点是A、B、C的三角形,记作“△ABC”,读作“三角形ABC”。
三角形两边的和大于第三边。
2、三角形的高、中线和角平分线
3、三角形的稳定性 三角形具有稳定性。
三角形中的三条重要线段:角平分线、中线、高
角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
说明:①三角形的角平分线、中线、高都是线段; ②三角形的角平分线、中线都在三角形内部且都交于一点;三角形的高可能在三角形的内部、外部,也可能在边上,它们相交于一点。
二、三角形的边和角
三边关系:三角形中任意两边之和大于第三边。
由三边关系可以推出:三角形任意两边之差小于第三边。
三、三角形内、外角的关系
三角形的内角和等于180°。
直角三角形的两个锐角互余。
三角形的一外角等于和它不相邻的两个内角之和,三角形的一个外角大于任何一个和它不相邻的内角。
三角形的外角和为360°。
四、等腰三角形与直角三角形:
等腰三角形:有两条边相等的三角形称为等腰三角形,
相等的两边叫做等腰三角形的腰,三条边都相等的三角形叫做等边三角形。
说明:等边三角形是等腰三角形的特殊情况。
直角三角形:有一个角是直角的三角形是直角三角形,它的两个锐角互余。
与三角形有关的线段练习题及答案
1、与三角形有关的线段有哪些?
2、长度为18cm的铁丝,一定能围成一个边长都为整数的三角形,有( )种围法,它的边长分别是
3、与三角形有关的线段
三角形ABC内有一点P,且CP=BC,连接AP、BP,求证:AB>AP.
答案
1、三角形的高 中线 角平分线
2、假设c大于等于b大于等于a
由三角形三边特点可知a+b>c,因为a+b+c=18 所以6小于等于c
3、角ABP=角ABC-角PBC
因为角ABC=180-角BAC-角ACB
所以 角ABP=180-角BAC-角PBC-角ACB
而角APB=360-角APC-角BPC
因为角APC=180-角PAC-角ACP
所以 角APB=360-(180-角PAC-角ACP)-角BPC=180-角BPC+角PAC+角ACP=180-角PBC+角PAC+角ACP
可以看到 角APB>角ABP (同样是180减去了角PBC但是 角ABP又减去了两个角,而角APB又加上了两个角 )
因为 大角对大边
所以 AB>AP
角角APB-ABP=BAP+2PAC+2ACP+PCB>0
所以角APB>角ABP,所以AB>AP